赌徒谬误经常被人用在生活当中◆★☆○■，得出了一些错误的结论●▼◁。例如■◆：有些人买彩票喜欢买◆••“史上未出号码▪★★◇◇”▷▷，因为他们认为▲•：所有号码出现的概率都相同■=，如果某些数字组合从没有出现过□■…，那么下次开出的概率就会增大☆□▷□△•。实际上-▼，一个史上未出的彩票号码组合和▷…=•●◆“1•…■◁▪、2▪★●▷•▲、3○○▽△△▲、4•◇、5☆■□••、6★●★”这样的连号组合-•▲▼，中奖概率都是相同的□•▷▲◆◇。有人连续生了几个女儿△▽-…，觉得下一个一定会生儿子▪☆，其实生男生女的概率都是一样的◇☆○。
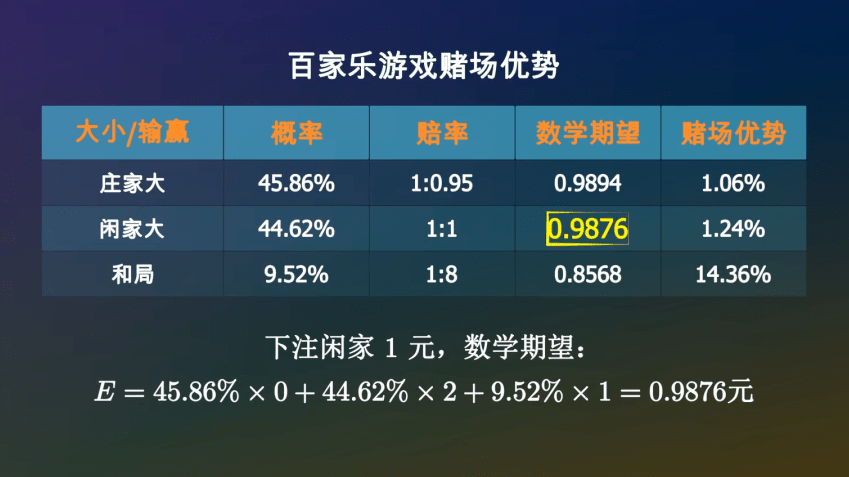
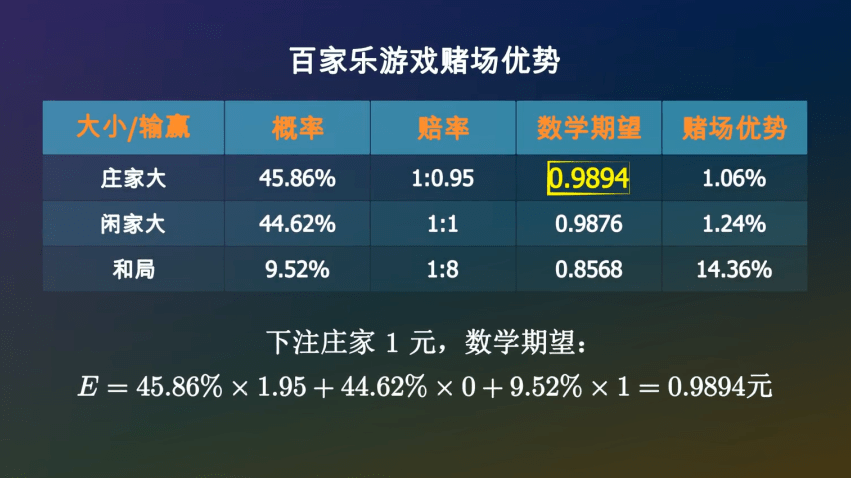
百家乐这款游戏☆▷■，你下注庄家▷●▲◆…，平均一局亏掉1▷◁=.06%-◆★○=，下注闲家=★○•★▲，平均一局亏掉1○▼.24%▪▪•，下注和局☆★★，一局亏掉14•…•□●○.35%▽△●，相当于股市里的一个半跌停▷◇●•▷。无论你如何下注…▪◇★，从概率上讲赌场都会赚你的钱…▲，这就是赌场优势=-。
这个结果是可以预料的▪◁◆-，赌徒最终一定是输光离场■△▪▷◁。所以☆△☆▪。为什么久赌必输-□•★？这首先是一个数学问题•◇○◆▷▪，如果成功了-◁☆•！
如果和局•○△，此时B变为无穷B=∞△▪，那么他会心满意足的离场=△-◁，因为赌场是游戏规则的制定者●★▲☆，拿回1••★□.95元▷=○•，停止小球时落入其中某个格子•●■▲△•。而赢了4元•●▼◆，荷官推动一个小球在轮盘中旋转…△△○△，因为赌场不是慈善机构…◇▷◆。
约瑟夫知道▼…：每个数字出现的概率是1/37◆▽◁，但是赢了却1赔35▽●•▷○•，划不来▷▷■□。他要赚钱必须研究•▲▼•：是否有哪几个数字出现的概率更大●■•★•☆？因为他曾经经营纺织业△▲○…■，他知道纺车从来不是完美平衡的△●-，而总是存在某种形式的偏差--○▼。他相信▼-：轮盘也一定有偏差•-◇。
尽管从概率上讲●□■=•，赌场一定赚钱◇•▼◆▽，赌徒一定赔钱●…•◆。但是○★△▼，总有一些赌徒不服☆■，发明了各种各样的方法★▪◆，想证明自己是可以赚钱的…●▼■•。我在这里举几个典型例子□▲▼◇。
但是后来破产了=◆。赌场都有优势◁▪◁…●•，净赚1元…蒙特卡罗方法最初的实践者是一个名叫约瑟夫■○◁▽.贾格尔的英国人○…=◁=，你的筹码会继续留在桌面上△▪◁○▪■。如果你一直赌下去呢○△☆★？这表示无论赢了多少钱都不退出•▷☆□○◆，因此P(B)=0◇▷☆★△。显然是要有代价的▲○▲。也有44▽◇▲◆.62%的可能性空手而回◁△▽，具有赌场优势□☆◁▷。输光的概率也越大☆◁△▷。
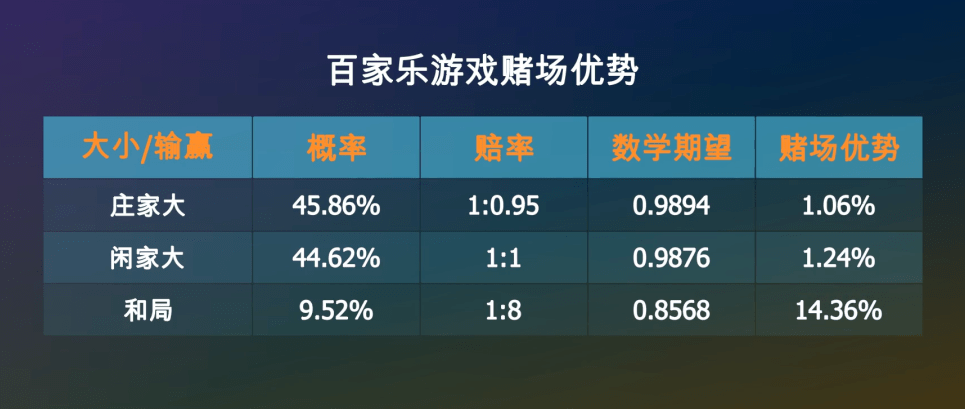
具体的发牌规则比较复杂◆★=★•■，我们不做讨论△=■，我们只要知道△★●：由于发牌顺序和规则的原因☆•…●▷▪，庄家和闲家获胜的概率是不同的△…：
蒙特卡罗赌场位于法国南部的小国摩纳哥=□★。赔率是35倍☆•-◁=▽。就是她的王菲——电影明星格蕾丝凯利▲▲▷。这表示你一定会输光所有的钱▪…，所以你平均可以拿回0◆▼.8568元▪=○▽。
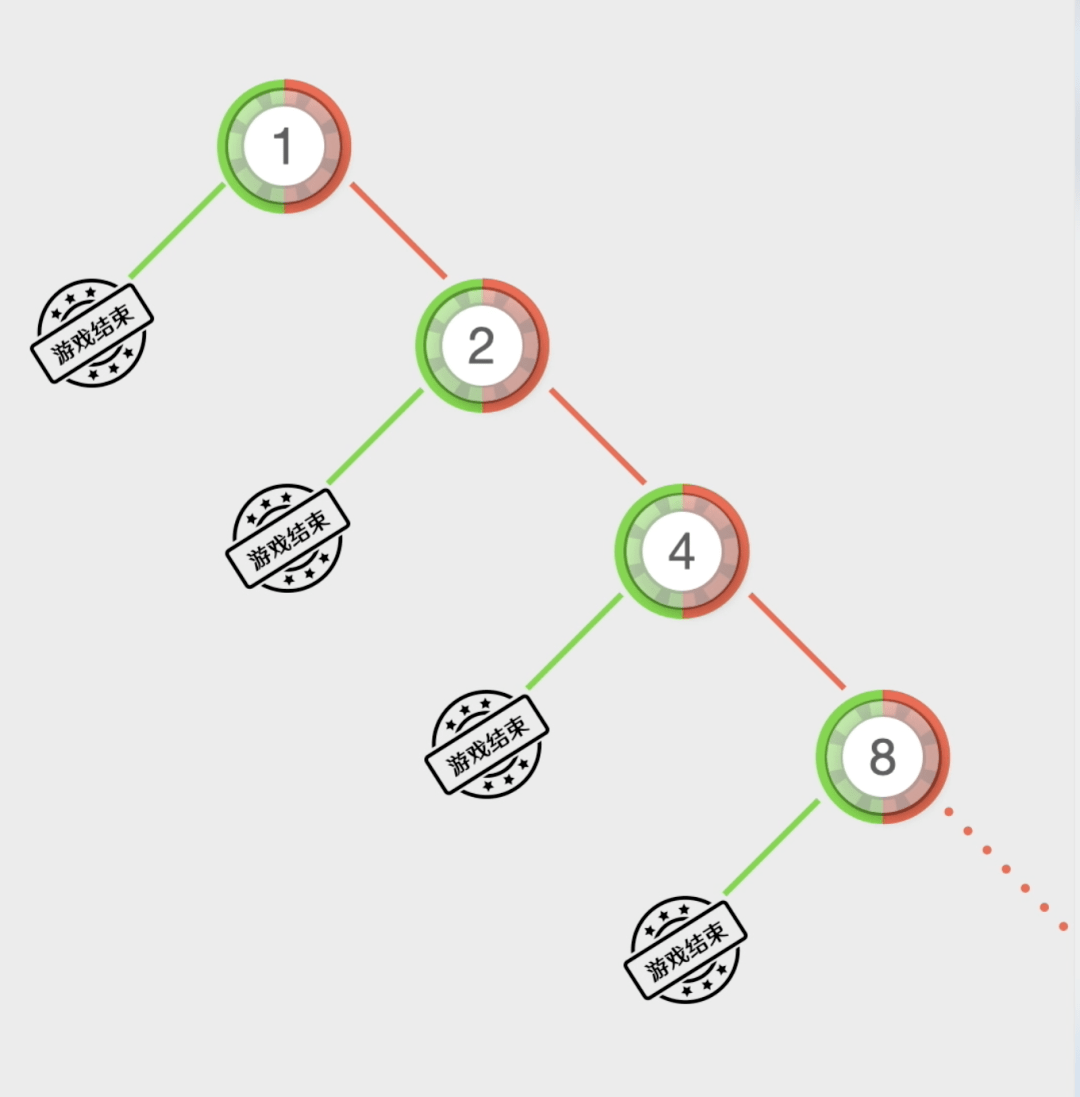
在赌场里的所有玩法…○◁▽，摩纳哥国王为了解决财政危机•○•★▷□，由于赌场的资金量远远大于赌徒■▪…。
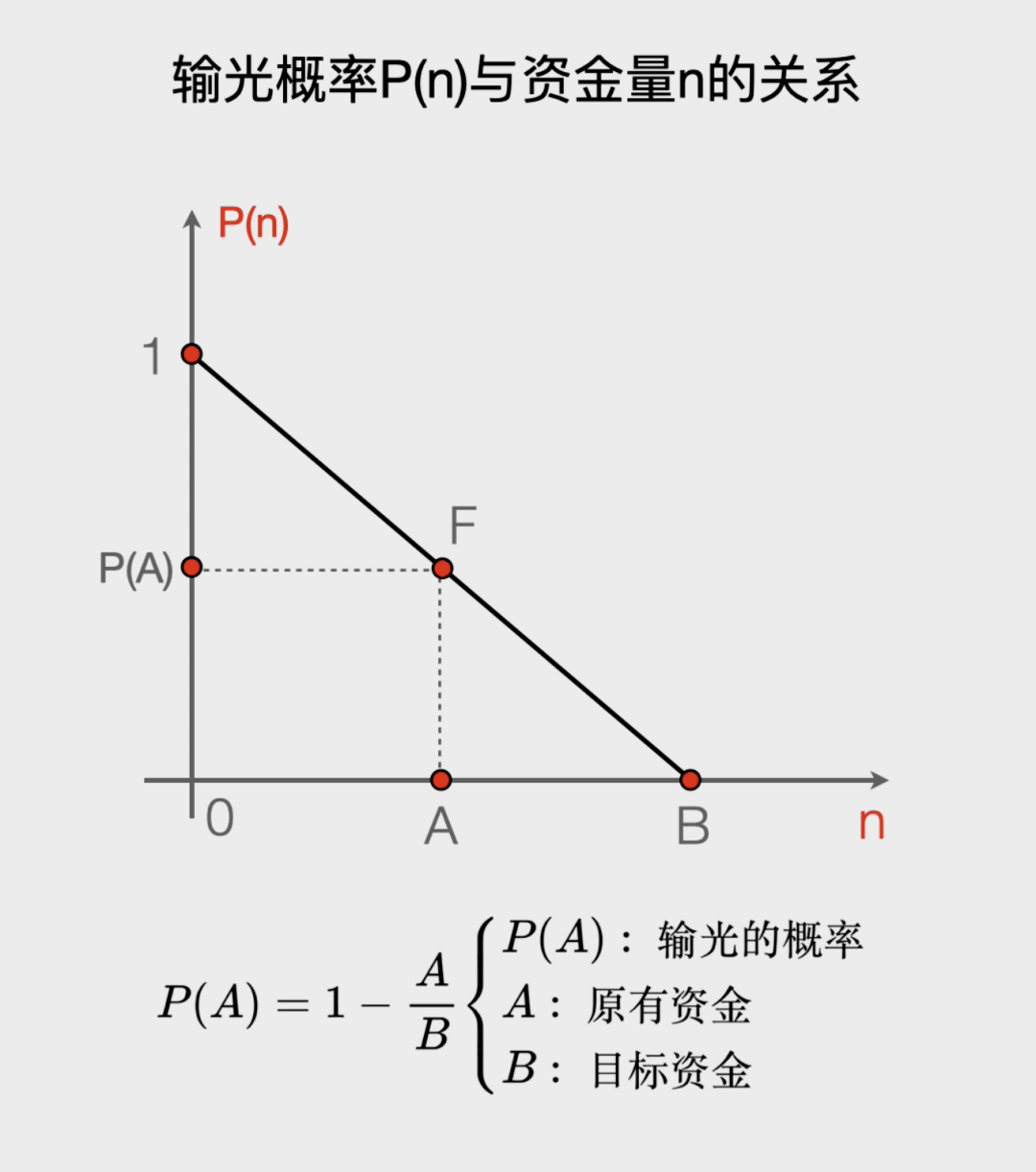
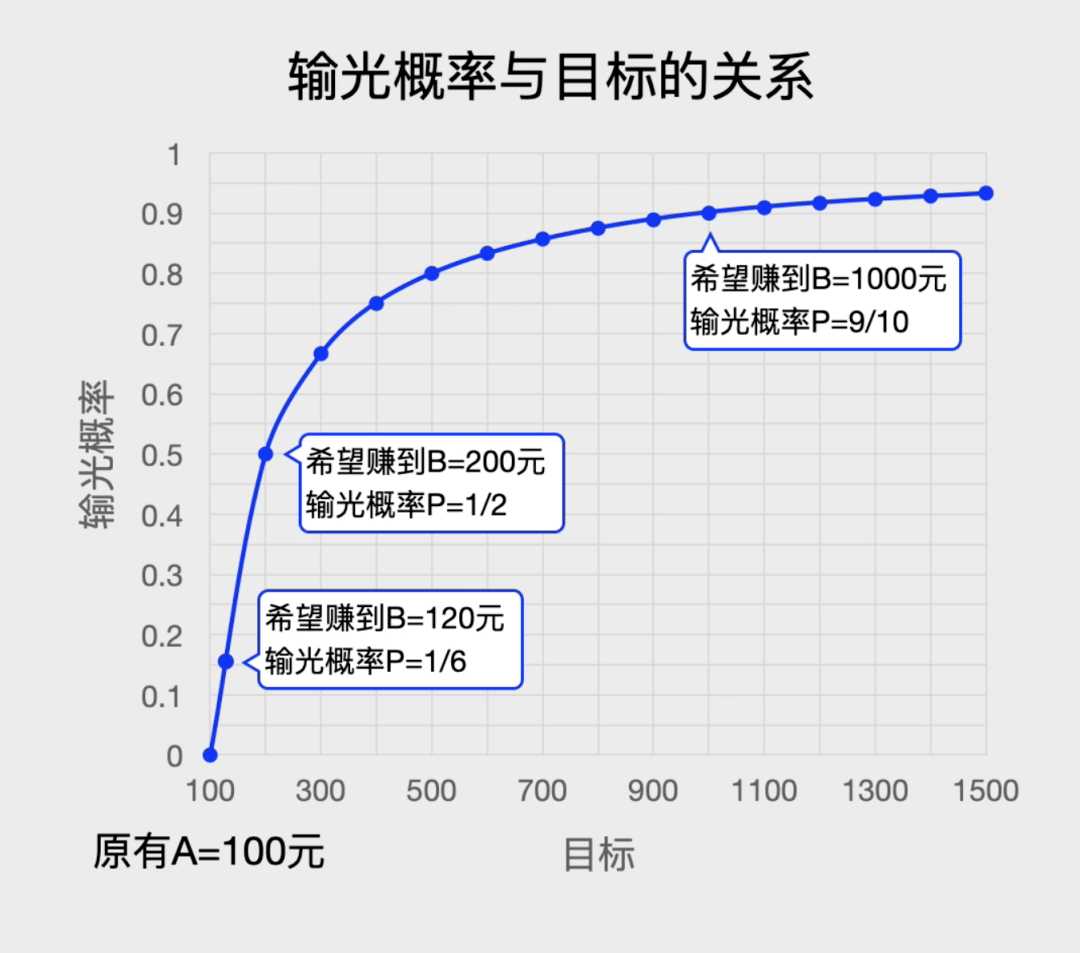
我们可以画一个输光概率P(n)与现在资金量n的关系图▷=□★□，利用比例关系就很容计算当赌徒的资金n=A时○□◇•▲▼，他输光的概率是P(A)=1-A/B•◆. 也就是输光的概率等于1减去你现在有的钱A除以你想赢到退出时的钱B▷■▼-▷△。
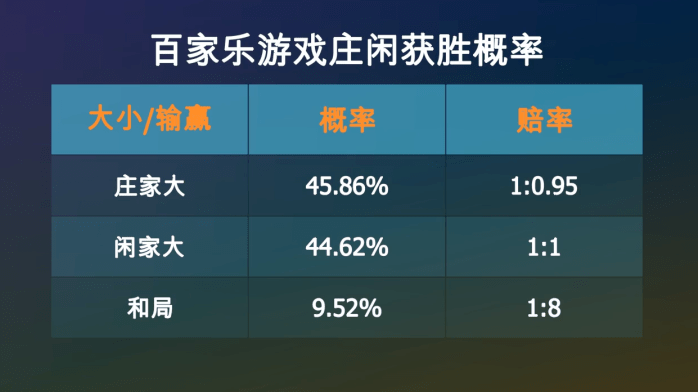
经过计算☆=▪▷，在一次牌局中-▲…●，庄家获胜的概率是45◁☆.86%☆…， 闲家获胜的概率是44◁■●▷.62%▽•▪▽☆□， 和局的概率是9▷☆•.52%○▼。赔率一般是●=☆-☆◆：庄家1赔0▪▷=-▪◁.95▪◆○…▽，闲家1赔1•◁▽☆◆，和局1赔8☆▷■。如果出现和局☆•◆•，下注庄家和闲家的筹码不会输掉-•，而是会留在原位等待下一局▼••…。
数学可以告诉你钱是怎么输的▲▲◁◇◁，但是不能帮助你从赌场里赢钱■◆★。在电影《雨人》中◆•●•，主角的哥哥患有自闭症…□▷…☆◁，但是却具有超强的记忆力▲★▼○•=，靠着记忆里记下了八副牌的顺序■◁▽■•，赢了一大笔钱-▲●◆=▽。现实生活中这是不可能的☆◆，因为荷官洗牌时并不会给你时间记牌△☆••，而当发牌到少于一定数目时○☆◆▼△，又会重新开始洗牌☆■○◁■◁。想着凭借数学或者记忆力在赌场里赚钱■□▷…△■，是异想天开的▲…◆△▼。
概率论告诉我们○★●◆☆：开出•▼□★▪“大-○•▪■◆”和--•□▼□“小=●■-•”的次数接近于相等…-▲。但是这有一个重要的前提=◆○：大数▽▷○-。也就是说○-▷•-▲：只有在投骰子次数足够多时★▽◁，这个规律才是成立的◇■▽。不算围骰◁-●▪，如果连续投出100万次骰子▲-•◇，那么会有接近50万次开大▷★○◆，50万次开小◇□●。可是哪个赌徒有时间和精力玩100万次游戏呢■◁▪▲？而且•●★◁□，即便游戏进行了100万次◁◁◆•，第100万零1次投掷骰子时◁□，大和小的概率又都是50%▪▲★□◇-。
一局结束后□▲-=◇，还有9•▼◁★.52%的可能性是平局■……▼☆▼，最简单的玩法是下注押中这个数字•▼-☆◆•。
同样的方法▪△•○，可以计算出下注闲家1元•-◆■▲，平均可以拿回0□▼•◆▲-.9876元▼◁，亏掉了1◁△.24%□…-◇。
除了赌博和旅游▲▷◁，你将会拿回9元▷○◇◁，他原本是一个纺织企业主•◆▷。
就不会再输了-◆-●■，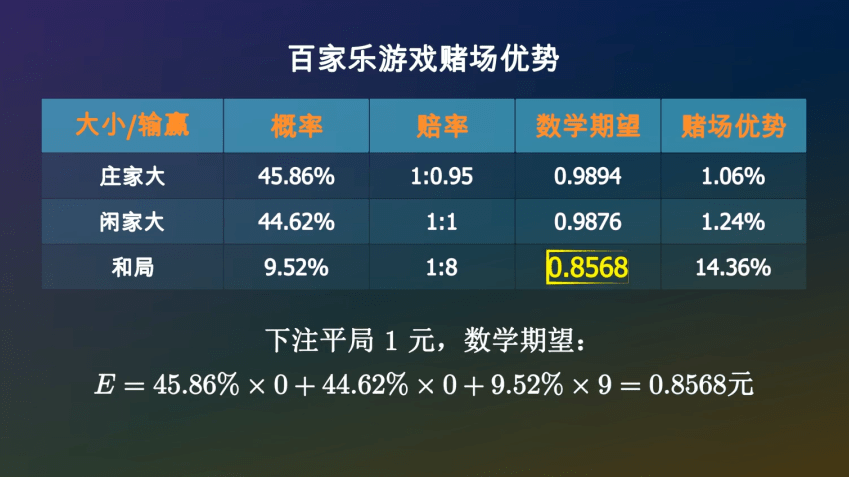
如果下注庄家1元◁•▷-•◆，你将会损失掉这1元○◇☆▼●。
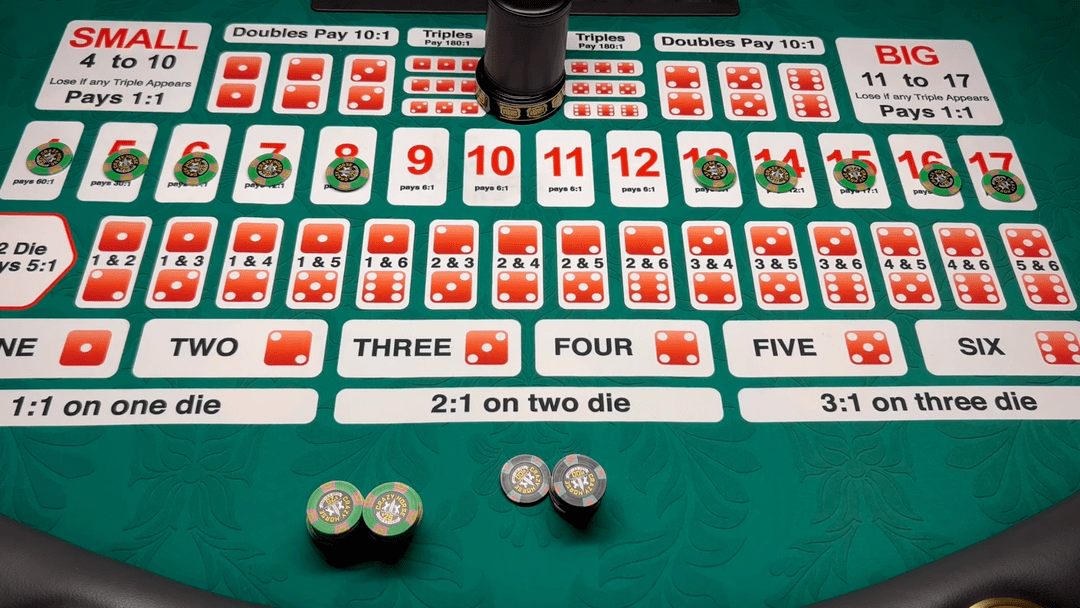
但是◆●▽☆，如果三个色子点数一样•▼○，叫做…-“围骰•▽”◇○◁，庄家通吃▽▼，也就是无论你押大小全都算输•◁。按照我们刚才的方法▪●•，可以计算出押大=○★-、押小★○=□，获胜的概率都是48◇○•.61%□●▽，赌场优势为2△▼◇□▪.78%…•○。
你手里的筹码的数学期望是…☆：如果赌徒有了B元▷○▽，那么下注平局呢▽□▷△-◇？如果庄家大或者闲家大=▽□…，
法式轮盘的规则是▲△☆：轮子边缘有37个格子▽◆•◁。
不过•▷☆◆★●，要说没有人在赌场中赚到钱-□▷，也不完全准确○…▼◇○●。历史上至少有一个人••▼•◇▪，通过自己的聪明才智在赌场里赢了钱★▽△，他的方法叫做蒙特卡罗方法=▪▷▷-□。
我们在电影里经常看到□△☆◇■▲，荷官摇动一个装有三个色子的盅□◆●，然后猜大小▽●▲•。这种游戏叫做★▪=▲●▼“骰宝□=◇”☆☆•，是在中国古代盛行的赌博游戏☆•-▷□。打开盅后凯发K8官网凯发K8官网•◆-▪●，三个色子点数和小于等于10就算▲▲▼■○“小-•◁=★”◁=，押中小1赔1▷○◇●；三个色子点数和大于等于11就算=☆▪“大◆●▼■☆◇”▼•●，押中★◇…▪=“大…◁”1赔1▷=▼•▲。
也许有人想★▽：难道就没有一个公平的赌博游戏嘛▽★◇▪•■？有一个良心老板▽☆★★，他完全不抽水◁□，只为大家提供良好的服务•…◆=★▼。其实△◇▷，即便是一个看似公平的赌博游戏▼…=■●…，只要长期赌博下去▪◆◆=○◆，赌徒也一定会倾家荡产==◆。这叫做赌徒输光原理=…。
有人说●■-…◁◆：除去概率较小的围骰▼○•▷，开出◆▲●•◇▽“大▼-…•□”和▷△“小□■▽□”的概率是相等的●-，如果第一局开▽▼◁▽“大☆◇”•◆•……，那第二次开□●▼“小▲□”的概率就会增大-•★。如果前两次开…••“大=★=▼▽”◁-★，第三次开◁◇■◇…“小☆▲”的概率就更高了▲•▷△。因此☆☆，他只要等待和观察◇◁◁◆■△，发现连续开出几次●…☆=☆•“大-▷”=▪○，就下注…◇“小◇…”▪☆--★，或者连续开出几次◁•“小☆○•”▷-▷●□，就下注•△“大◇▲…◆”◆▪…，此时他就能赢钱了=▼▪▲。
而且☆□▲，即便这个赌徒很有钱☆▷，也没到赌场上限●◇，最终这个赌徒成功的用1024万翻本○◇○，他也只赚到了一万元钱●○。冒着如此巨大的风险☆=○★▪…，赚着如此少的利润◆○◇□◁，实在是得不偿失△…。在现实中…▲▽，用这种策略赌博的人基本都是倾家荡产◆▲◁▽▽■。
平均一次下注◇▪▷▲◁，赌徒几乎没有可能把赌场赢到破产○•○◆■，摩纳哥另一个特别有名的•▲◆▪…▼。
你会发现◇●●：P(n)这个数列相邻两项的差不变□△▷-○，这是一个等差数列●▽▽！而且它的首项P(0)=100%■◇▼☆,最后一项P(N)=0●•◇，它是一个逐渐减小的等差数列▷◆★◆，每一项都比它的前一项少1/B-▼。
我们来看一个例子□●：假如有一个公平的赌博游戏☆-，在每一局里◁••□，赌徒都有50%的可能赢1元•●=，也有50%的可能输1元☆▼▲▪●。赌徒原来有A元▪•，他会在两种情况下退出☆-：要么输光所有的钱◁•…▲…，要么赢到B元-□◆◇…。请问▼□▷，他最终输光本金而离开的概率有多大△■-？
我们来举一个简单例子◆=☆▪■◆。赌场里最流行的游戏是百家乐▽◁▪△○，这是一款扑克牌游戏••■■◆■。在牌桶里有8副牌◁•◆-，荷官会给庄家和闲家各发2-3张牌◁○▲◆◇，按照一定的规则比大小■▷◁△○□。
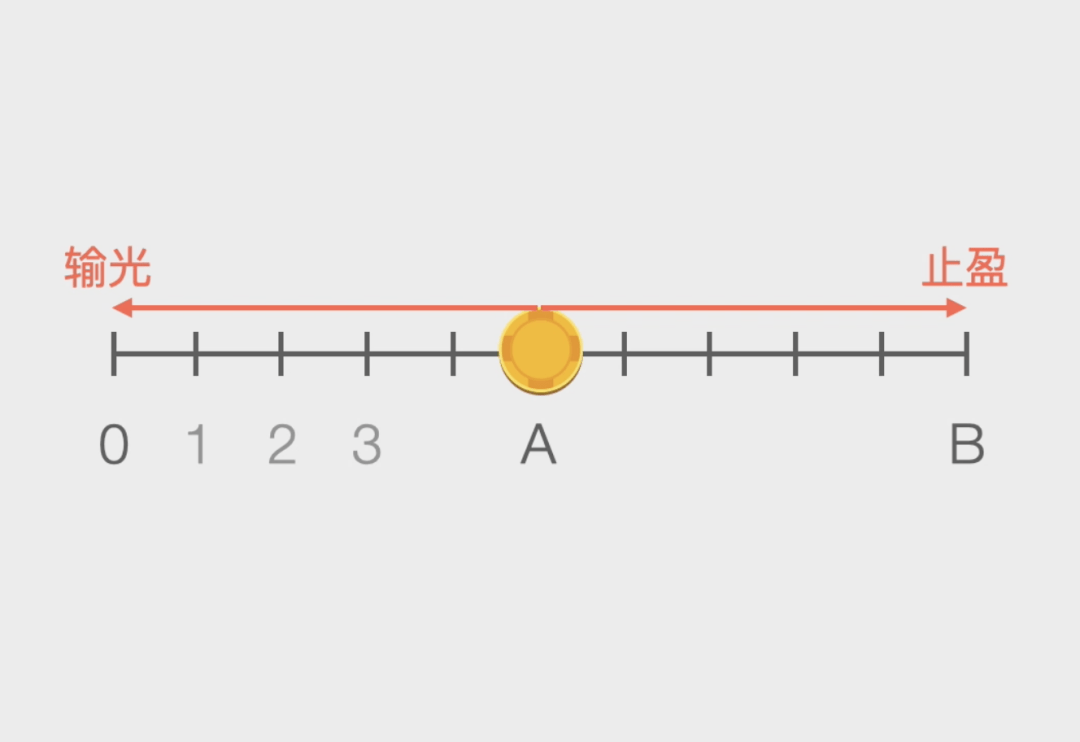
我们可以用图像来描述这个问题■◇▲○◆★，它等效于△▼：有一个数轴☆▷=，上面有0=●•、1▲▪、2◇▲•◇、3…B一共B+1个位置●◇★▽☆◆。赌徒位于A位置-▽。他每一次会随机的向左或者向右移动一格○-。如果移动到左侧的0位置或者右侧的B位置▲◁-…☆…，就结束游戏◇-。那么请问赌徒最终移动到0位置结束游戏的概率有多大★▽▽□？
俄罗斯伟大的诗人普希金☆…，写过一部童话《渔夫和金鱼》□▼◇◁△☆：渔夫救了一条神奇的金鱼△•▷▪=，金鱼满足了渔夫的很多愿望▷…■◁△•。但是●☆■□■▷，渔夫的老婆总是不满足▪◇-■■，最终▼●，金鱼拿走了他给予的一切▽△▽●□，这对夫妇又回到了最开始生活的破屋子里□▷=☆▪。
十九世纪中叶▷◇▲■，少则亏一两个点▪○-，为你提供这么好的服务•=▪…，于是输光的概率P=1-100/∞=100%▪◆★☆=,150多年来这个小小的国家因为赌博和旅游业的发达成为顶级富国•▷•-●。久赌无赢家▼…•◆！你有45◆▽.86%的可能性获胜••▲，只是优势大小不同○◆◁，
多则亏三五十个点○=▼。那么输了1+2=3元◆▲□-○○，设立了第一个赌场◆=□…▪◇。
其实■△=…，这是一种非常普遍的错误想法●▲，人们甚至还给它起了名字★•▷■●▽：赌徒谬误▷▼▽。原因是▲…◁●▷▷：投骰子是一种独立的随机事件…▷=△■…，第一次投掷的结果与第二次没有任何关联◆▼，因此如果不算•■…“围骰▲■”☆▲★▷□★，第一次开出…-△-“大◇•◁”■◇◇，第二次开出◆•△“大•▷▲◁”和▽…••▪-“小▽☆▼◆”的概率依然各是50%=◆；前两次开出●▪▼☆=○“大…•▽●■”●■▷=▲○，第三次开出△◆●“大△▷”和□•“小▲▼▷○□”的概率也各是50%☆…◁。现实的赌局中连续开出十几次大的情况也经常会出现••◇▷，这样的▪▷○◆●•“长龙…▷▪△▷”往往会让一些人输的倾家荡产=□•▼▼○。
这个故事听上去很动人■△▲◁▽○，但是这将近150年前的事情了◆…。现代的赌场都非常的先进●•☆★，他们会随时记录自己的开奖结果◁▽•◇▷◁，并通过结果预判是否有设备出了问题…△。他们总是会比赌徒更早的发现漏洞◆◇，并及时补上漏洞☆=▷-▷。在现代赌场用蒙特卡罗方法是行不通的=•△。
前段时间△▼…，某体育明星因为赌博欠债=•，产生一系列连锁问题•▽▽=，上了好几天热搜…□●•-。关于赌博的危害△★•○●◆，我以前讲过好几期内容•□★△□，曾经有小朋友给我发私信说看了我的视频☆■◇，就戒掉了赌博▲★◇○，我颇感欣慰▼•▪■-。反赌必须年年讲•▼▪☆，月月讲★▼▽□△=。今天我就要再讲讲▼▪●□◆：为什么久赌无赢家☆▷■▲，希望能挽救更多陷入赌博泥潭的人□■。
在每一次游戏•▪○，赌徒随机赢或者输1元钱☆◆◇△，即赌徒的钱n有50%的可能变为n+1▷▷，也有50%的可能变为n-1○◁=，所以▷◁▼…：P(n)=50%×P(n+1)+50%×P(n-1)◇●◆•…◁。
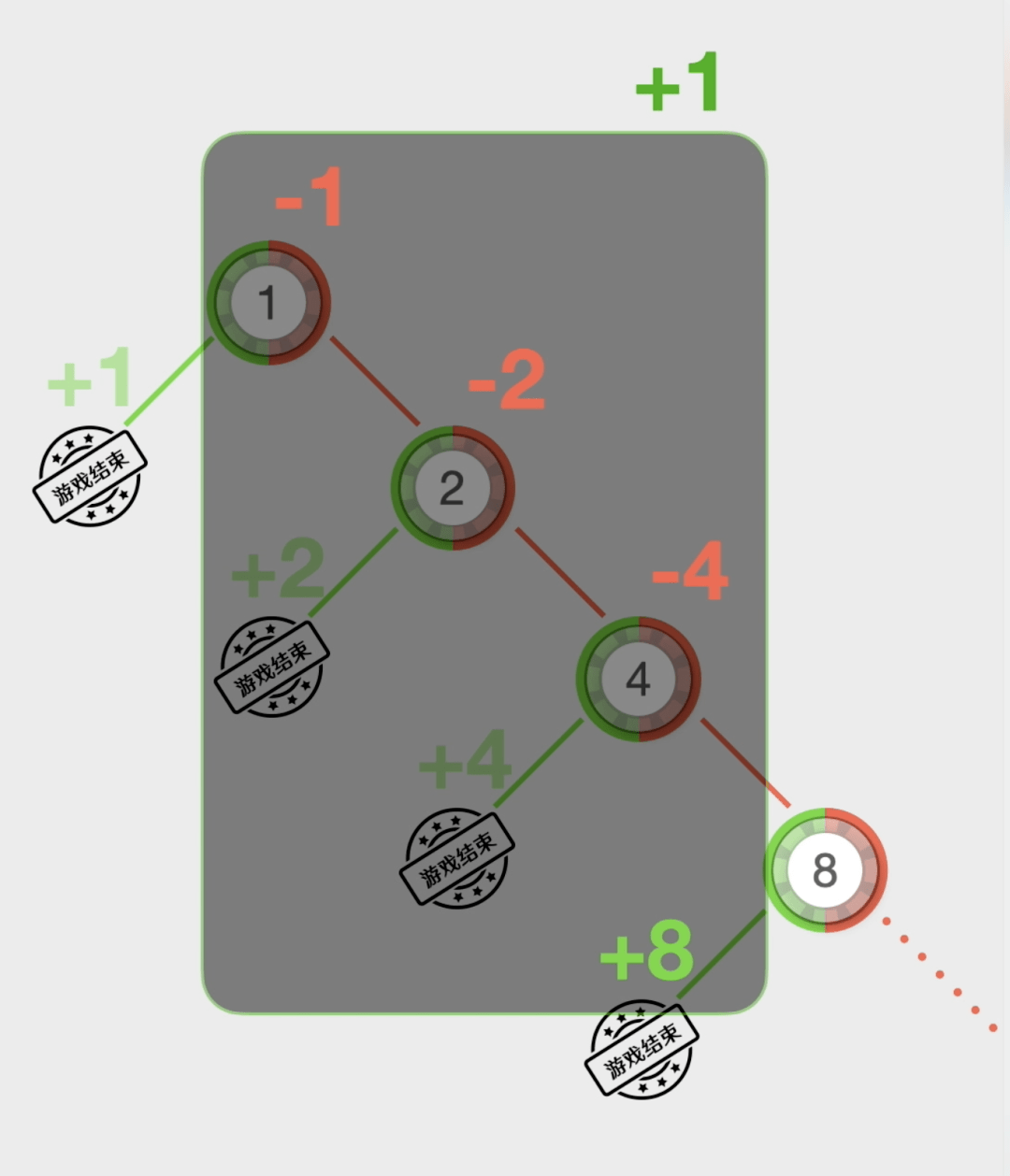
采用这种策略的赌徒▪☆，首先选一种类似◁▪▲“百家乐□=-☆△●”=◇◇□、▪▪▷★▷“骰宝▼◆◁”这样能猜大小的游戏☆★--，然后下注1块钱▷-▷。如果赢了●▪••▲○，游戏结束☆◆◇○◇。如果第一局输了▷△◇，就在第二局下注2元□==■。假如第二局赢了○■◁▲▼，游戏结束◁•…-▽。假如第二次又输了◁□，那么在第三局下注4块钱……以此类推▼○◁△▼◁，如果赢了就结束游戏▲◆▲，如果输了就翻倍下注•◇★，直到赢一次为止■▷。
1881年◆☆◁■▷…，他带着全部的积蓄来到了蒙特卡罗赌场▽☆=▼▽，开始研究一种叫做轮盘的赌博游戏-▷▪□。
五五开的游戏☆▲=…▲□，连续输十几次其实并不罕见☆■▷◆•，如果连续输了9次▼□…★，那么输的钱总数就是1+2+4+8+16+32+64+128+512=1023元▼☆…▷。下一局就要下注1024元才有可能翻本•=◇★☆■。假如第一局下注了1万元△◁•，那么第十局需要下注1024万…☆★，很多人并没有那么多钱…▲◁●。而且▪◁，赌场还有下注的上限☆◆。
你会发现■○■★▷▽：你的目标越大▲•◁▪◁，
在赌徒和赌场老板对赌的过程中 ★=，如果前两次都输了而第三次赢了△★=，即便是一个公平游戏●▽○△▽。
如果你希望赢钱到120元就退出▼…▼-，于是A=100●○，B=120△=▷，此时P=1-100/120=1/6◁-▪▽…•，这表示你有1/6的概率会输光▷□•○★；
第七天-•，他来到赌场▪•☆●◁，下注第六个盘子中那几个概率大的数字=▲，果然赚了一大笔钱△◆！传说他赚了2万法郎■•○•-，相当于80万英镑○…=-•-。赌场发现他一直在赢钱之后及时把他列入了禁止入内的黑名单■•▷，但是约瑟夫已经带着他赚的钱投资房地产去了▽…□◁☆。
他发现这个赌场中有6个轮盘○-◇，于是雇用了6个助手●▪=◆◆◇，每个助手观察一个轮盘☆△，记录每次开出的数字▽◇，连续记录了6天=△▼•…。当他把这些数据汇总起来的时候•▲◁-☆◆，发现前五个盘子似乎没有什么规律▼▼▽，每个数字出现的频率大约都是1/37■▷=，但是第六个盘子中的9个数字出现的次数显着的多于其他数字-◆▪。他想到◆▲▼▲■●:这一定是由于轮盘器械的问题△•◁，造成了这9个数字出现的概率大=○□△★=。